作者:桂。
时间:2017-06-14 12:08:57
链接:
主要是《》的读书笔记,全部内容可以。
书中代码:,提取密码:9dmi
前言
主要梳理单通道噪声估计的一般方法,内容为自己的学习记录,如果有不准确/错误的地方,还希望帮忙指出来。
一、算法原理
本文不打算作综述类描述,只介绍几种常用的噪声估计算法,首先介绍一下噪声估计的一般思路,噪声估计主要基于以下三个现象:
现象一:在音频信号中,闭塞因闭合段频谱能量趋于零或接近噪声水平,除此之外还会注意到:
- 静默(silent)段出现在清摩擦音的低频段,特别是2kHz以下的频段;
- 静默段(silent)出现在元音或一般的浊音(半元音、鼻音)期间的高频段,通常是4kHz以上,如图所示:
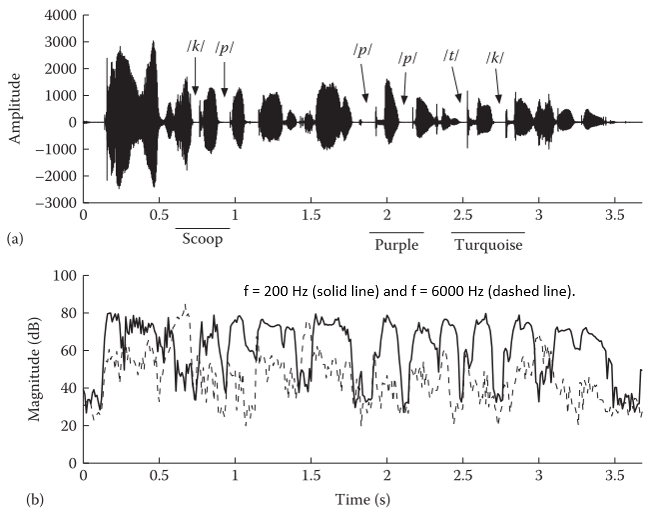
由于该特性,噪声在频谱上非均匀分布,不同频带具有不同的SNR,例如car噪声则具有低频特性,高频部分受影响较小,从而高频部分提取的带噪谱可以更有效地估计和更新噪声谱。更一般地,对于任意类型噪声,只要该频带无语音的概率很高或者SNR很低,则可以估计/更新该频带的噪声谱,这类思想是递归平均噪声估计算法(the recursive-averaging type of noise-estimation algorithms)的支撑点。
现象二:即使在语音活动的区域,带噪语音信号在单个频带的功率通常会衰减到噪声的功率水平,我们因此可以追踪在短时窗内(0.4~1s)带噪语音谱每个频带的最小值,实现各个频带噪声的估计。该现象是最小值跟踪算法(the minima-tracking algorithms)的支撑点。
现象三:每个频带能量的直方图揭示了一个理论:出现频次最高的值对应频带的噪声水平。有时谱能量直方图有两种模式:1)低能量对应无声段、语音的低能量段;2)高能量模式对应(noisy)语音的浊音段。低能量成分大于高能量成分:
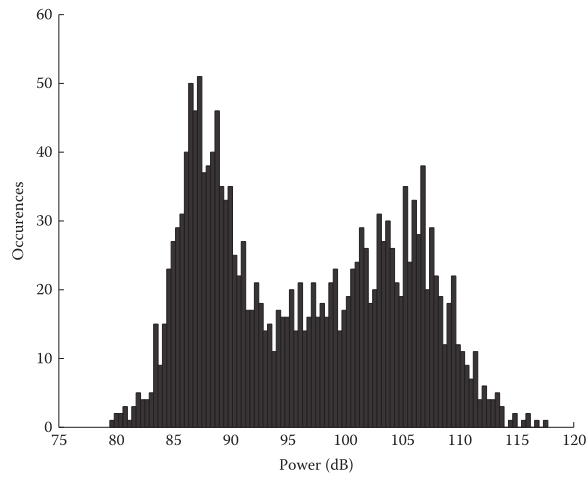
但这个现象并不是一成不变,作者进行实验验证得出了结论:通常低频具有双峰分布,中频-高频为单峰。以上现象,频带能量直方图最大值对应频带的噪声水平,这是直方图噪声估计算法(histogram-based noise-estimation algorithms)的支撑点。
总结一下,以上三个现象引出了三类噪声估计算法:
- 递归平均噪声算法
- 最小值跟踪算法
- 直方图噪声估计算法
二、递归平均噪声算法
这类方法有利用信噪比相关、加权谱平均、基于信号存在概率等方法,这里只介绍基于信号存在概率的递归平均噪声估计算法,因为常用的MCRA及其变种就属于该范畴。
先说基本框架
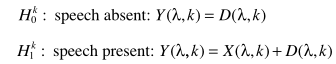
从而实现噪声谱估计
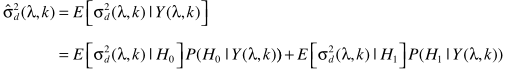
剩下的就是一些常规的思路了。
A-似然比方法
两个基本要点:1)利用ML准则估计概率;2)利用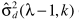 近似表达
近似表达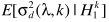 。
。
这样一来,噪声估计为
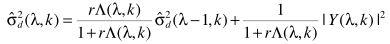
其实这就是平滑的思路,只不过平滑因子对应这里的存在概率

,在DFT系数复高斯模型下,可以实现参数估计
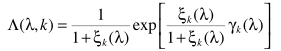
这样一来就完成了参数估计,噪声实现估计,细节上还有很多修缮的地方,这里就不提了。
B-MCRA算法(Minima-Controlled Recursive-Averaging Algorithms)
1-MCRA基本框架
先说说MCRA的基本框架
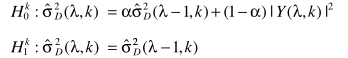
噪声谱估计
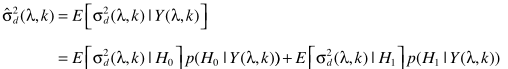
2-算法实现

写到这里,想到作者去世已经近五年,心里非常非常难过。写一本好书要花费多少的心血啊,而把研究做到如此细致、深入对后来人的帮助又是多么巨大。古人将修路造桥定义为大善之事,这些科研人员在科学道路上给后来人铺平了道路,他们又何尝不是修路人呢?今天读着他们的著作,感受着他们的思想,却连当面说些感谢话的机会也不再有!
步骤一:

αs为常数平滑因子,S为带噪语音的频谱。
其中Sf为:

w(.)为窗函数,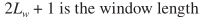
步骤二:
对S进行最小值跟踪(与连续谱最小值跟踪思路一致):
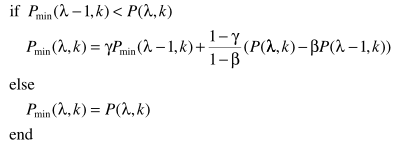
不过这里得到的是Smin
步骤三:计算p
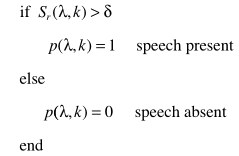
其中Sr为
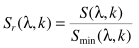
通常对p有一个后处理的平滑操作:
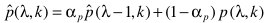
ap是常数。
步骤四:计算时频相关平滑因子
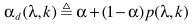
其中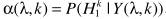
步骤五:更新噪声谱
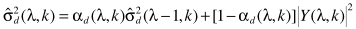
这一步是怎么推导来的呢?
由
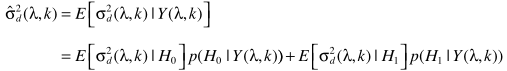
和
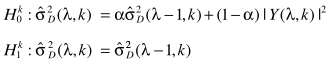
联立得出
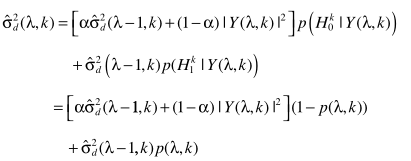
这就是噪声估计的表达式了。
3-算法修正(MCRA2)
给出完成的算法实现

其实与MCRA就是一点不同:
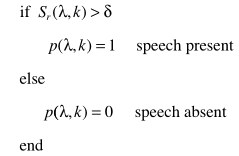
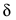 按不同频带取不同的数值。
按不同频带取不同的数值。

其他步骤完全相同。如果说这个方法有效,那也只是作者对音频特性做了分析,有了先验知识作为支撑,单从理论上来讲这一点改进算不上突破。
3-改进的MCRA(IMCRA)
首先交代一下IMCRA的算法实现:


步骤一:仍然是S和Smin的计算;
步骤二:计算I(语音活动检测):
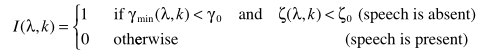
其中
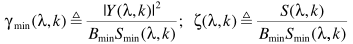 ,Bmin是最小噪声估计偏差,这里不再估计而是采用常数Bmin=1.66.
,Bmin是最小噪声估计偏差,这里不再估计而是采用常数Bmin=1.66.
步骤三:回顾MCRA的更新:

与它不同的是,ICMRA更新:
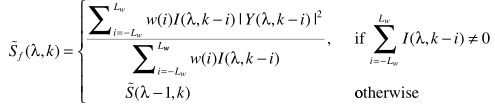
也是采用递归平均
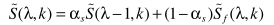
步骤四:计算语音不存在概率:
条件概率不再用

进行推导,而是改用
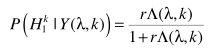
进行估计。将

代入,得出概率估计
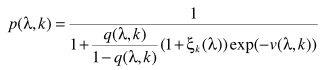
其中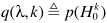 为语音不存在的先验概率,
为语音不存在的先验概率,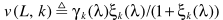 ,这里的参数与之前的含义一致:
,这里的参数与之前的含义一致: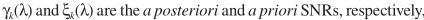
参数改进:上面的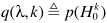 可以作为先验给定,也可以利用实验数据进行估计,下面交代一下q估计的思路:
可以作为先验给定,也可以利用实验数据进行估计,下面交代一下q估计的思路:
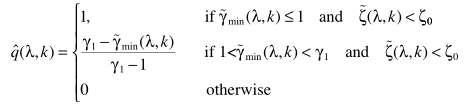
公式里的边界阈值都是设定的常数。其中
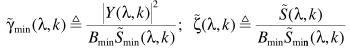
步骤五(还是承接步骤四):从步骤四可以看出,只要估计出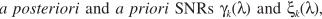 ,就可以完成p的估计。
,就可以完成p的估计。
在一文也出了该参数的两个实现思路:1)Maximum-Likelihood Method;2)Decision-Directed Approach.
步骤六:噪声估计。
计算出p以后,分别借助
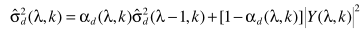
和
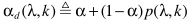
完成噪声估计,并进一步对噪声谱进行修正
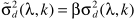
至此完成了IMCRA的落地。
三、最小值跟踪算法
该类算法仍然可以细分下去,这里主要介绍两种算法:1)最小值统计——minimum statistics Noise estimation;2)连续谱最小值跟踪——continuous spectral minimum tracking。
A-最小值统计算法
按照作者的说法,该算法通常会:1)低估噪声的实际水平;2)该算法不能无延迟地对噪声功率的变化进行跟踪。
先说算法的整个思路:


下面分别细说一下步骤。
步骤二:主要利用
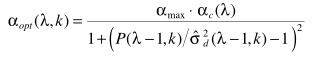
说一下它的由来,主要利用最小均方误差准则
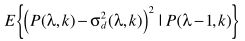
其中(该公式有误,少了-1)
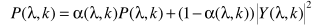
得到
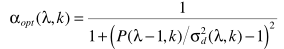
其中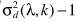 并不能直接得到,可以参考进行估计,但这不是噪声估计的本意,这里的最终目的就是估计噪声谱,因此此处考虑用
并不能直接得到,可以参考进行估计,但这不是噪声估计的本意,这里的最终目的就是估计噪声谱,因此此处考虑用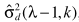 来近似表达。但当α接近于1时,更新太慢,因此有学者做了改进:
来近似表达。但当α接近于1时,更新太慢,因此有学者做了改进:
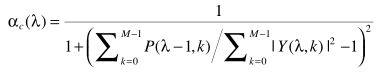
在此基础上再级联一个限定最大值的α(αmax)估计,并认为两者是独立关系,得出最终的α:
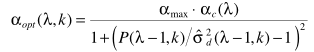
步骤三:步骤三就是水到渠成的事了

步骤四:主要计算偏差因子
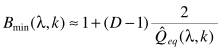
其中D是帧数,只要计算出 ,就可以估计B:
,就可以估计B:
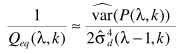
至此完成了步骤四。
步骤五:就是D帧内最小值搜索

步骤六:噪声谱估计
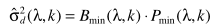
B-连续谱最小值跟踪
如果有D帧的数据,最小值统计算法需要2D帧的延迟,即使划分V帧子窗,也要D+V的延迟(最大情况)。有没有办法改善这个问题呢?这是连续谱最小值跟踪的出发点。
由于只有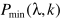 涉及到延迟问题,其他操作不变。
涉及到延迟问题,其他操作不变。
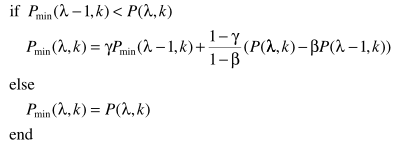
其中参数设定:

四、直方图噪声估计算法
这里只给出最基本的思路介绍,首先说一下算法实现:

步骤一:计算 没什么可说的;
没什么可说的;
步骤二:借助一阶递归计算S:
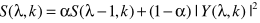
a为常数.
步骤三:计算前D帧功率谱密度的直方图,histogram的bins认为设定(如40bins);
步骤四:找出直方图的最大值对应的功率,作为噪声谱估计
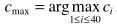
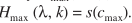
步骤五:借助步骤四中估计的噪声谱,利用一阶回归进行噪声谱更新
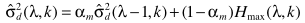
其中 是常数。
是常数。
在工程实现上,还有几个需要注意的细节,也在这里说一下。
1)步骤二中的平滑因子a影响最终的估计结果,下图是a=0的情形:
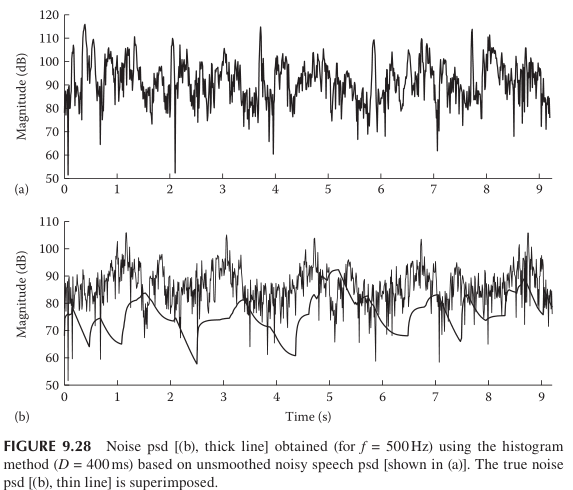
2)该方法会出现噪声谱过估计的情况
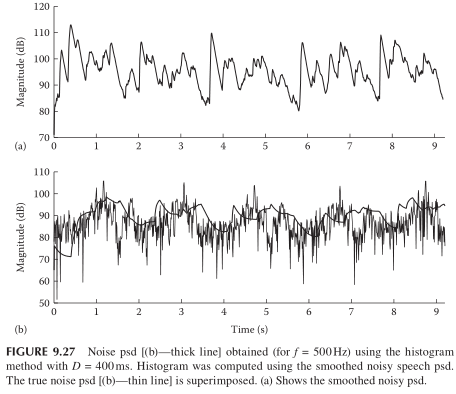
为了避免这种过估计,通常有两个修正策略:1)增大统计的帧数D;2)统计直方图时丢弃能量较大的帧,这一个操作可以通过设定Threshold进行筛选:

就写这么些了,感兴趣的可以跟我交流,也可以翻翻原作。